-
1
×InformationNeed Windows 11 help?Check documents on compatibility, FAQs, upgrade information and available fixes.
Windows 11 Support Center. -
-
1
×InformationNeed Windows 11 help?Check documents on compatibility, FAQs, upgrade information and available fixes.
Windows 11 Support Center. -
- HP Community
- Archived Topics
- Tablets and Mobile Devices Archive
- Re: how to solve an intergral equation of circular function ...
Create an account on the HP Community to personalize your profile and ask a question
02-28-2017 06:10 PM
how to solve an intergral equation of circular function with domain restrictions?
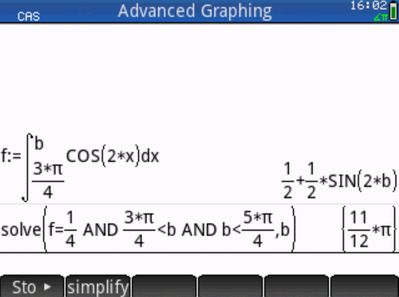
for example, find the value of b for the equation
int(cos(2x), 3*pi/4,b)=0.25, where 3*pi/4<b<5*pi/4
I enter:
solve(int(cos(2x), 3*pi/4,b)=0.25, b)|3*pi/4<b<5*pi/4
but the above HP Prime command did not work. Later I asked several Maths teachers, they did not know how to deal with them too.
How do we figure out it?
note: this question is from a VCE quesiton (Victoria certificate equation in australia)
03-02-2017 09:00 AM - edited 03-02-2017 09:40 AM
Hello,
The CAS in Prime behaves more like all the "real" CAS systems out there. Namely, you make an assumption about a variable, then do the operation and continue working with those assumptions. Thus the "planned" way to do this is:
1. make your assumption (note your variable needs to come first - it is "storing" the assumption into the variable).
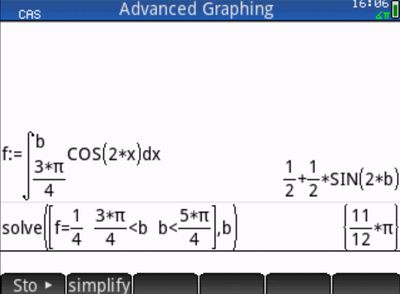
assume( b>(3*π/4) AND b<(5*π/4)) <--- "3*pi/4<b" doesn't work because b is on the right - keep your variable to the "left" of the assumption
2. Now you have the assumptions stored, try your original input:
solve((int(cos(2*x),x,3*π/4,b)) = (1/4),b)
3. Out pops the expected result.
4. Note that you have assumptions stored in b, and they will remain until you remove them. To do so, run purge(b) and it will remove the assumption values stored on b.
I personally thought this was kind of strange and wonky at first. Then, I understood why it behaves this way. Using this method of making assumptions on variables allows much more powerful assumptions to be made and is why all the high power CAS systems follow the same type of methodology. You can do things like assume a variable is a specific object type (real, complex, member of a subset, etc) and other much more complex things that would just be very difficult to do in a single | statment.
In addition, you very often continue working with those restrictions on that variable as you continue working the problem. It kind of follows the way you would do a mathematical proof in some ways - you start applying assumptions about variables, and then work your way through the problem.
HOWEVER, you can do this in a single operation. If you really do want to make a temporary assumption, follow the same recommendations regarding your variables ONLY being on the left side. This will ALSO work:
(solve((int(cos(2*x),x,3*π/4,b)) = (1/4),b)|((b>(3*π/4)) AND (b<(5*π/4)))) <--- (note b in the | always appears to the left of the < or > or >= or <> and similar - don't put your variable on the right side)
Out pops the same result.
Feel free to ask some more questions if you get stuck! 🙂
Although I work for the HP calculator group as a head developer of the HP Prime, the views and opinions I post here are my own.
03-02-2017 10:52 AM
@Tim_Wessman wrote:
You can do things like assume a variable is a specific object type (real, complex, member of a subset, etc) ....
That is interesting, Tim.
How do you assume that a variable is real?
03-02-2017 12:18 PM
Here's some examples of possible assumptions:
assume((a>=2 and a<4) or a>6)
assume(x>0); additionally(x,float);
assume(x,integer);
assume(x,complex);
The main 3 categories most applicable here are: "float", "integer", "complex".
about(x) would return the assumptions made about x currently.
Also, as a note to the original poster - I'm working with the CAS author regarding accepting things like 0<b directly rather then requiring it to be flipped, and also things like 0<b<2 or similar directly. That might be a possible future improvement that can be made. Thanks for the question!
Although I work for the HP calculator group as a head developer of the HP Prime, the views and opinions I post here are my own.
03-03-2017 12:07 PM
@Tim_Wessman wrote:Here's some examples of possible assumptions:
assume((a>=2 and a<4) or a>6)
assume(x>0); additionally(x,float);
assume(x,integer);
assume(x,complex);
The main 3 categories most applicable here are: "float", "integer", "complex".
about(x) would return the assumptions made about x currently.
Thank you.
I see that the example:
assume(x,integer)
is given in the user manual but not in the built- in Help.
I found out that another way of writing is:
assume(x,2) or assume(x,DOM_INT) and that we can get the types by e.g.
type(3.56) which returns DOM_FLOAT.
03-05-2017 02:21 PM
Dear Tim,
thank you.
I have solved the question by inputing
command (1): "assume( b>(3*π/4) AND b<(5*π/4))"
command (2) "(solve((int(cos(2*x),x,3*π/4,b)) = (1/4),b)|((b>(3*π/4)) AND (b<(5*π/4)))) "
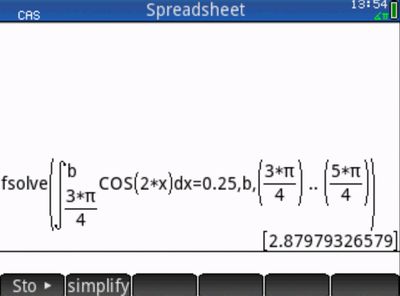
But if i change 1/4 into 0.25 in the command (2), then no solution is found, why?
03-05-2017 05:29 PM
That changes it from an exact, symbolic system into one that is "approximate" with non-exact numbers. Basically, keep decimals out of your symbolic calculations as that throws the CAS into a mode where it will use numerical algorithmns and similar. Most CAS systems behave this way - it can be confusing to new users though.
Although I work for the HP calculator group as a head developer of the HP Prime, the views and opinions I post here are my own.
| Question | Author | Posted | |
|---|---|---|---|
| 03-29-2025 11:46 AM | |||
| 07-12-2024 04:45 AM | |||
| 02-18-2025 02:35 PM | |||
| 03-04-2014 10:44 AM | |||
| 08-28-2023 04:06 PM | |||